Números Primos e Fatoração com a Escala Cuisenaire

Anne Michelle Dysman, Jéssica Rama e Marcella Candido

Este módulo instrucional destina-se ao ensino de números primos e fatoração utilizando a Escala Cuisenaire. O material concreto é utilizado para promover a aprendizagem significativa, pois a comparação dos tamanhos das barras da Escala Cuisenaire fornece um registro concreto para a ideia de múltiplo, possibilitando a compreensão dos números primos como relacionados àqueles tamanhos que não podem ser “decompostos” em certa quantidade de barras com uma medida menor (não unitária). Estas atividades foram desenvolvidas para utilização com turmas de sexto ano, como método para rever os conceitos de número primo e fatoração. Os conceitos de múltiplos e divisores começam a surgir neste módulo instrucional de forma natural, preparando os alunos para as atividades dos módulos instrucionais sobre múltiplos, mmc, divisores e mdc, também disponíveis neste site. Caso a escola não disponha do material concreto (Escala Cuisenaire), sugerimos uma forma de confeccionar uma versão de baixo custo.

As atividades deste plano dividem-se em 3 etapas:

– Atividade 1: Observação de múltiplos e reconhecimento de números primos

– Atividade 2: Existência da decomposição dos naturais em fatores primos

– Atividade 3: Algoritmo da fatoração

O trabalho aqui proposto pode ser executado de forma individual ou em grupos (sugerimos a execução em duplas). O professor deve explicar oralmente as atividades descritas neste plano e cada aluno deve registrar suas observações e resultados em uma ficha do aluno (em anexo).

Objetivos

– Explorar o conceito de número primo de forma significativa, através do uso de materiais que dão concretude às ideias de múltiplos e divisores.

– Introduzir os conceitos de múltiplos e divisores de maneira natural (sem explorar muito tais conceitos) preparando os alunos para trabalharem com os módulos instrucionais Entendendo Múltiplos e MMC e Entendendo Divisores e MDC, nos quais tais aprofundaremos a aprendizagem de tais conceitos.

– Ensinar o conceito de fatoração em primos e atribuir significado ao algoritmo usual para fatoração.

Materiais utilizados

– Cada grupo (ou aluno, caso seja realizada individualmente) deve receber um kit de barrinhas da Escala Cuisenaire com as quantidades discriminadas na tabela abaixo. Caso a escola não disponha deste material, é possível produzir versão de baixo custo com uso de um dos seguintes materiais: varetas pega-balão, emborrachado (E.V.A.) ou papel cartão. Par isso siga as instruções do Guia de Produção de Material Cuisenaire (versão baixo custo).
– Ficha de acompanhamento (uma por aluno).

Etapas do trabalho

As atividades deste plano dividem-se em 3 etapas:

1ª atividade: Reconhecimento de números primos

2ª atividade: Existência da decomposição dos naturais em fatores primos

3ª atividade: Algoritmo de fatoração

Descrição do Material

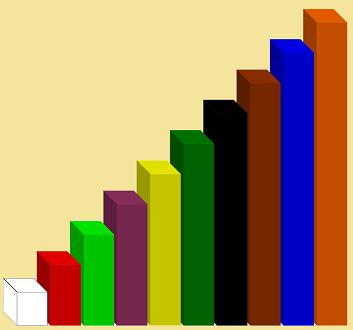
A figura a seguir ilustra as barrinhas da Escala Cuisenaire que serão utilizadas ao longo deste módulo instrucional. São 10 cores que correspondem aos números de 1 a 10. Os tamanhos das barrinhas também variam de forma proporcional ao número que representam.

Atividades

1ª atividade: Observação de múltiplos e reconhecimento de números primos

Objetivos: Introduzir de forma natural a ideia de múltiplo através de observações com o material concreto e possibilitar aprendizagem significativa do conceito de número primo.

Materiais: Kit com material Cuisenaire, ficha de acompanhamento.

1º PASSO – EXPLORANDO O MATERIAL

– Deixe que os alunos manuseiem o material concreto por alguns minutos.

– Peça aos alunos que tomem uma barrinha de cada cor e que comparem as barrinhas.

– Pergunte a eles quantas barrinhas tomaram.

– Peça que ordenem por tamanho as barrinhas.

– Pergunte o que podem observar quanto aos tamanhos das barrinhas. Os alunos devem notar que, tomando como unidade a menor barrinha (que é um cubinho) para cada número n de 1 a 10 há uma barrinha cuja medida é exatamente n unidades (não esperamos que os alunos expressem desta forma, apenas que observem o fato e o relatem com suas palavras). Se eles não observarem este fato por conta própria, peça que alinhem barrinhas brancas ao lado de cada uma das barrinhas coloridas, de forma que possam realizar a observação desta relação.

– Defina a menor barrinha como unidade.

– Explique aos alunos que todas as comparações agora serão feitas a partir dessa barrinha (branca). Peça que eles completem na ficha de acompanhamento a tabela que representa a correspondência entre o número representado por cada barrinha e sua cor.

Hora de registrar: Exercício 1 da ficha de acompanhamento.

2º PASSO – OBSERVAÇÕES SOBRE MÚLTIPLOS E DIVISORES

– Uma cor por vez, os alunos devem tomar uma barrinha da cor da vez e buscar alguma outra cor de tal que possamos reproduzir o comprimento da barrinha da vez utilizado alguma quantidade de barrinhas desta outra cor. Por exemplo, a barrinha verde-escura que representa o número 6. Podemos substituí-la por três barrinhas vermelhas que representam o número 2, ou por duas barrinhas verde claros que representam o número 3, conforme ilustrado na imagem abaixo. Recomende que eles tentem realizar este exercício sem utilizar as barrinhas brancas e só as utilizem quando não houver outra opção.

Hora de registrar: Exercício 2 da ficha de acompanhamento. Oriente os alunos da seguinte forma: Para as barrinhas de 2 a 10 cujos comprimentos podem ser obtidos através da justaposição de barrinhas de mesma cor, anotar ao lado do número a multiplicação correspondente à operação realizada com as barrinhas. Por exemplo, se para obter o comprimento da barrinha verde escuro (seis) o aluno utilizou duas barrinhas de cor verde claro (correspondente ao número 3), deve registrar na folha de atividades ao lado do número 6 a operação “= 2 x 3”. Nos casos em que tiveram que utilizar barrinhas brancas, devem registrar também (por exemplo: “5 = 5 x 1”)

– Realizar a mesma verificação indicada acima para comprimentos equivalentes aos números de 11 a 20. Para isso deve-se, sucessivamente, justapor uma barrinha de 10 a barrinhas de 1 a 10 e, para o comprimento obtido, procurar um grupo de barrinhas de mesma cor que, quando justapostas resultem no comprimento correspondente ao número em questão, como vemos abaixo para o número 12 (a imagem abaixo ilustra “12 = 2 x 6”).

Hora de registrar: Continuação do exercício 2. Anotar na ficha de acompanhamento as multiplicações que correspondem às equivalências obtidas no item acima para os números de 11 a 20 (por exemplo, se o aluno usou 3 barrinhas roxas para representar o número 12, devem registrar ao lado do 12 “= 3 x 4”).

– Introduzir os termos múltiplos e divisores utilizando como exemplos os produtos registrados na ficha de acompanhamento. Nesta etapa recomenda-se que estas conceituações sejam feitas através de exemplos: 6 = 2 x 3, então 6 é múltiplo de 2 (e também de 3), pois pode ser obtido pela multiplicação de 2 por 3. Igualmente, 12 é múltiplo de 4 e de 3 porque pode ser representado pela multiplicação destes dois números. Para conceituar divisores usamos o mesmo método: 2 é divisor de 6, pois 6 pode ser dividido por 2 (sem sobrar resto). Também 3 é divisor de 6. Para 12, temos que 4 é divisor de 12 porque 12 pode ser dividido por 4 (com resto zero). Neste momento ainda não exploraremos mais profundamente os conceitos de múltiplos e divisores (o que será realizado nos módulos instrucionais “Entendendo Múltiplos e MMC” e “Entendendo Divisores e MDC”).

Hora de registrar: Realizar o exercício 3 da ficha de acompanhamento.

3º PASSO – IDENTIFICANDO NÚMEROS PRIMOS

– Peça aos alunos que verifiquem para quais dos comprimentos de 1 a 20 eles não conseguiram realizar o passo anterior sem utilizar as barrinhas que representam uma unidade. Por exemplo, para a barrinha amarela que representa o número cinco não há nenhuma outra cor (que não seja a branca ou a própria amarela) que, justapondo apenas barrinhas desta cor, nos dê o mesmo comprimento. Também para o número 13, obtido pela justaposição da barrinha laranja com a verde-claro, a única maneira de obter seu comprimento utilizando uma única cor de barrinha é utilizando as barrinhas brancas que representam a unidade. Os alunos devem circular na ficha de atividades os números para os quais isto ocorre. Abaixo vemos que é este o caso do número cinco (barrinha amarela).

Hora de registrar: Continuação do exercício 2 da ficha de acompanhamento: Para os números de 2 a 20 no execício 2 os alunos devem circular aqueles que não podem ser representados como produto de outros naturais (sem usar o 1).

– O professor deve explicar que os números circulados são chamados de números primos e explicar que um número recebe este nome sempre que é maior que 1 e só possui como divisores 1 e ele mesmo;

Hora de registrar: Os alunos devem responder à questão 4 da ficha de acompanhamento.

2ª atividade: Existência da decomposição dos naturais em fatores primos

Objetivos: Observar a existência da decomposição em fatores primos para os números naturais de 2 a 20 e fazer com que os alunos percebam empiricamente que todo natural maior que um pode ser decomposto em fatores primos.

Material Utilizado: Ficha de acompanhamento.

– Peça aos alunos para, nas multiplicações que registraram no exercício 2, circularem todos os números primos que encontrarem (por exemplo, se registraram “8 = 2 x 4”, devem circular o 2);

– O professor deve propor ao aluno a seguinte tarefa: obter qualquer dos números que não são primos na lista utilizando apenas números primos e operações de multiplicação. Assim, por exemplo, partindo de

o aluno deve ser instruído a buscar na própria lista de números em sua ficha uma forma de substituir o 6 por um produto de números primos. Encontrará 6 = 2 x 3, e substituindo na multiplicação, ficará com

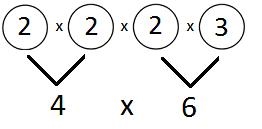
– Uma vez realizado o exercício que acabamos de propor, o professor deve explicar ao aluno que essa forma de escrever um número que não é primo como produto de números primos chama-se decomposição do número em fatores primos (lembrar que cada termo em uma multiplicação é chamado de fator) e que, assim como ele obteve a decomposição em fatores primos de cada um dos números de 1 a 20, essa decomposição também pode ser obtida para qualquer outro número natural maior que 20.

3ª atividade: Algoritmo da fatoração

Objetivos: ensinar o algoritmo da fatoração de forma significativa.

Após as atividades 1 e 2 acima o professor deve ensinar o algoritmo da fatoração utilizando-se, para isso, da própria ficha de acompanhamento onde encontra-se circulada a lista de todos os primos de 1 a 20. Vamos utilizar como exemplo a fatoração do número 140.

– Pedimos aos alunos que anotem o número 140 e ao lado coloquem a barra vertical para a fatoração como na ilustração abaixo:

– Olhando na ficha de atividades, qual o primeiro primo que está circulado? É o número dois. O número 140 é divisível por dois? Sim, 140 = 2 x 70. Então anotamos:

– Agora ficamos com o número 70. Ele também é divisível por 2? Sim, 70 = 2 x 35. Anotamos:

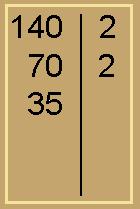
– E o número 35, é divisível por 2? Não. Qual o próximo primo em nossa lista? É o número 3. O número 35 é divisível por 3? Não. Qual o próximo primo da nossa lista? É o 5. E 35 é divisível por 5? Sim, 35 = 5 x 7. Registramos:

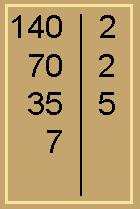
– Ficamos com 7, que já é primo. Logo temos:

o que significa que

140 = 2 x 2 x 5 x 7

como podemos ver no lado direito da barra da fatoração.

Hora de registrar: Como exercício o professor deve propor que os alunos fatorem os números de 21 a 40 e completem a ficha de atividades circulando os primos entre 21 e 40 e anotando as fatorações ao lado dos números que não são primos. Para que esta atividade seja mais dinâmica, sugerimos que o professor sorteie alunos para fatorarem no quadro cada um destes números com ajuda dos colegas da turma. Com uso de uma cartolina é possível também aproveitar esta atividade conjunta par fazer uma tabela com as fatorações destes números.

Após a realização das atividades deste módulo, os alunos estão prontos para trabalharem com as propostas dos módulos instrucionais Entendendo Múltiplos e MMC e Entendendo Divisores e MDC.