
Helena Calvo, Liliane Branco e Anne Michelle Dysman
Esta atividade destina-se a introduzir o conceito de frações tomando como foco os dois aspectos a seguir:
– relação entre partes e todo;
– localização das frações na reta dos números reais.
Utilizaremos como recurso pedagógico as réguas de frações. Algumas escolas possuem este material, o qual também pode ser adquirido em lojas que comercializam brinquedos pedagógicos. Contudo, como o custo deste material é relativamente alto, fornecemos as instruções para a produção de uma versão alternativa do mesmo, confeccionada com canudos pega-balão. (Também podem ser usados canudos comuns, mas o material fica menos resistente). Para as escolas que possuem kits de réguas de frações, sugerimos que aproveitem o material disponível. Caso a escola possua apenas um kit, este pode ser utilizado como material do professor. Nesse caso, sugerimos que a escola providencie kits para os alunos utilizando os canudos de forma a manter as mesmas cores do material que será utilizado pelo professor. Caso a escola não possua o material, recomendamos que, além dos kits dos alunos, seja providenciado também um kit maior (com canudos mais longos e de maior espessura), que será usado pelo professor para explicar as atividades.
Sugerimos, para a realização do trabalho que os alunos sejam divididos em duplas e que cada aluno (ou cada dupla) utilize um jogo de réguas (denominaremos assim também o material feito com canudos).
Objetivos
– Introduzir o conceito de fração de forma significativa;
– Construir, através de observações sobre o material concreto, a noção de equivalência entre frações;
– Ensinar a identificar a localização de frações na reta numérica;
– Estabelecer a relação entre frações e suas representações decimais.
Materiais utilizados
– Réguas de frações (um kit por aluno ou dupla);
– Listas de exercícios e acompanhamento fornecidas neste plano (uma por aluno).
Etapas do trabalho
1ª atividade: Representando Frações com as Réguas
2ª atividade: Comparando Frações, casos simples
3ª atividade: Encontrando Frações Equivalentes
4ª atividade: Simplificando Frações (e mais um pouco de comparação)
5ª atividade: Localizando Frações Próprias na Reta
6ª atividade: Localizando Frações Impróprias na Reta
Descrição do Material
A figura a seguir ilustra um kit de réguas de frações já nas cores que serão utilizadas ao longo deste módulo instrucional (estas cores podem variar de um fabricante para outro).
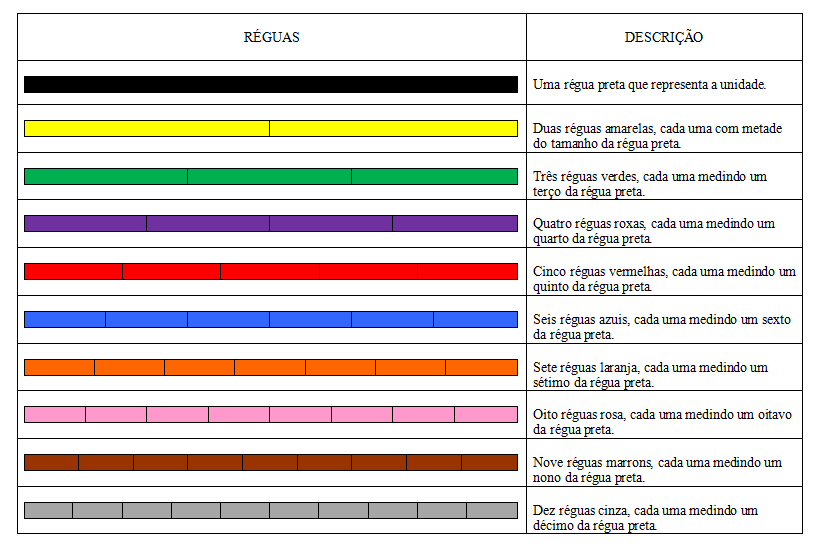
Atividades
1ª atividade: representando frações com réguas
Objetivos: Apresentar o material aos alunos, definir frações com base nas réguas e representá-las através da notação usual.
Materiais: Réguas de frações, ficha de atividades 1.
1º PASSO – EXPLORANDO O MATERIAL
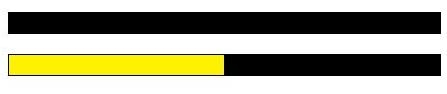
– Peça aos alunos que sobreponham as réguas amarelas à preta.
– Pergunte a eles quantas réguas amarelas eles utilizaram. (A resposta será duas.)
– Conclua com eles que a régua amarela cabe duas vezes na régua preta.
– Em seguida, peça a eles que repitam o procedimento com as demais réguas.
2º PASSO – DEFININDO A UNIDADE
– Defina a régua preta como unidade.
– Explique aos alunos que todas as comparações agora serão feitas a partir dessa régua.
3º PASSO – NOMEANDO AS RÉGUAS
– Peça aos alunos que sobreponham uma régua amarela à preta.

– Pergunte que pedaço da régua preta foi coberto pela amarela (espera-se que eles respondam “metade” ou “meio”).

– Explique que a partir deste momento a régua amarela será chamada de meio.
– Peça que sobreponham uma régua verde à preta.

– Pergunte que pedaço da régua preta foi coberto pela verde. Como no 1º passo dessa atividade eles viram que a régua verde cabe três vezes na preta, espera-se que eles respondam que uma régua verde cobre um pedaço que corresponde à régua preta dividida por 3. (Se esta observação não ocorrer, peça que eles coloquem outras réguas verdes lado a lado até obter o mesmo tamanho da preta.)

– Diga-lhes que a partir desse momento a régua verde será chamada de terço. (“Terço” porque se diz respeito a “três”.)
– Repita o mesmo procedimento para as demais réguas e conclua que estas serão chamadas de quarto, quinto, sexto, sétimo, oitavo, nono e décimo.
4º PASSO – DEFININDO FRAÇÕES A PARTIR DAS RÉGUAS
– Peça aos alunos que peguem duas réguas que representam “quintos” e as sobreponham à régua preta.
– Explique que a parte (ou fração) coberta da régua preta corresponde a dois quintos da mesma.
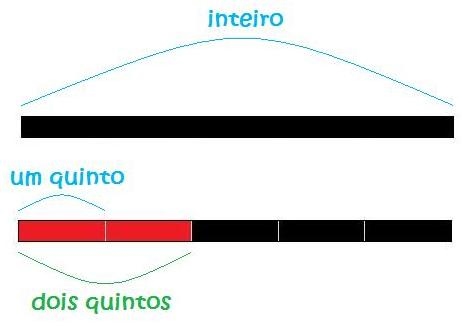
– Peça que peguem quatro réguas que representam “sextos” e as sobreponham à régua preta. Pergunte que fração dessa régua eles obtiveram. (Espera-se que eles respondam: quatro sextos.)
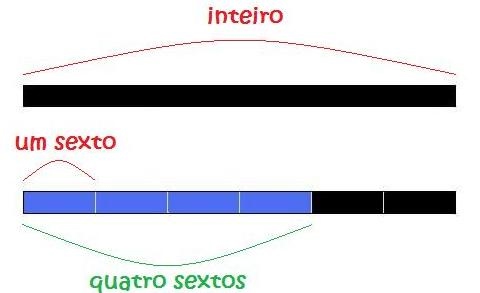
O professor deve seguir apresentando outros exemplos até que fique claro para os alunos o que está sendo feito.
- Hora de registrar: Após a realização deste passo recomenda-se que os alunos façam a atividade 1 da ficha de acompanhamento 1.
5º PASSO – INTRODUZINDO A NOTAÇÃO FRACIONÁRIA
Agora que os alunos já conhecem os nomes das réguas, o professor pode construir com eles a representação de fração:

– Explique que o termo numerador se refere à quantidade de réguas tomadas e que o termo denominador se refere ao nome dado a tais réguas.
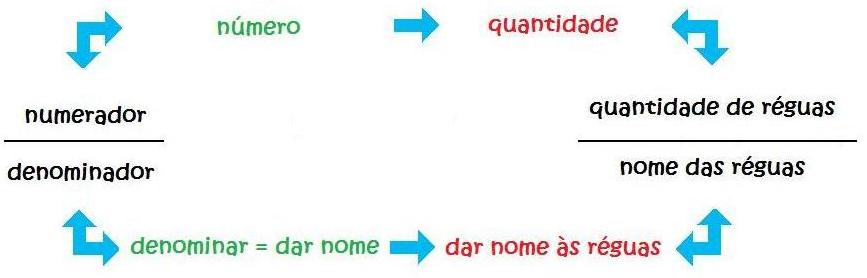
– Partindo do exemplo anterior, explique que dois quintos significa tomar duas partes de um total de cinco. Assim, o total de partes em que foi dividido o inteiro chama-se denominador (nesse exemplo, 5) e o número de partes tomadas chama-se numerador (nesse exemplo, 2).

Desse modo, chega-se à representação:
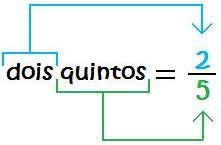
O professor deve apresentar mais exemplos para fixação até certificar-se de que os alunos compreenderam bem a representação das frações, seguem algumas sugestões:
– Junto com os alunos represente a fração obtida quando se toma três réguas roxas (três quartos): Três quartos: significa que o inteiro foi dividido em quatro partes iguais e foram tomadas três dessas partes. Isto é, o denominador é igual a 4 e o numerador é igual a 3.
– Junto com os alunos represente a fração obtida quando se toma sete réguas marrons (sete nonos): Sete nonos: significa que o inteiro foi dividido em nove partes iguais e foram tomadas sete dessas partes. Isto é, o denominador é 9 e o numerador é 7.
Se for necessário, apresente ainda mais exemplos ou exercícios sobre representação fracionária aos alunos.

Hora de registrar: Após a realização deste passo, recomenda-se que os alunos façam as atividades 2 e 3 da ficha de acompanhamento 1.
2ª atividade: comparando frações, casos simples
Objetivos: Comparar frações com e sem o auxílio das réguas
Material Utilizado: Réguas de frações
1º PASSO: FRAÇÕES COM DENOMINADORES IGUAIS
Exemplo: Comparar 1/3 e 2/3.
Para comparar estas frações os alunos deverão, inicialmente, representá-las com as réguas.
– Peça-lhes que representem as frações 1/3 e 2/3, utilizando o material, de acordo com o que acabaram de aprender. Espera-se que eles as representem da seguinte forma:

– Questione-os sobre os comprimentos obtidos.
– Pergunte qual é menor. (Acredita-se que todos responderão que 1/3 é menor do que 2/3.)
– Conclua que, nesses casos em que os denominadores das frações são iguais, a quantidade de réguas tomadas é que determina qual será a fração maior.
Em linguagem matemática:
1/3 < 2/3
Para melhor compreensão recomenda-se a realização de outros exemplos, tais como:
– comparar 2/5 e 3/5
– comparar 3/8 e 5/8
2º PASSO: FRAÇÕES COM NUMERADORES IGUAIS
Caso 1: NUMERADORES IGUAIS A 1
Comparar 1/2 e 1/3:
– Peça aos alunos que representem estas frações com as réguas e comparem tais representações.
– Explique que, assim como no passo anterior, uma fração será maior do que a outra se o comprimento total das réguas utilizadas para representá-la for maior que o comprimento total das réguas utilizadas para representar a outra fração.

Nesse caso, como ambos os numeradores são iguais a 1, basta comparar os comprimentos de uma régua meio e de uma régua terço.
Espera-se que os alunos concluam que:
1/3 < 1/2.
Comparar 1/4 e 1/8:
– Explique que, assim como no exemplo anterior, a comparação se dá entre frações cujos numeradores são iguais a 1. Então, para determinar qual é a maior fração entre as duas, basta comparar os comprimentos de uma régua quarto e de uma régua oitavo. Nesse caso,

1/8 < 1/4.
– O professor deve apresentar outros exemplos com numerador 1. O objetivo desta etapa é levar o aluno a perceber que sempre que m < n vale 1/m > 1/n.
– Devemos pedir aos alunos que expliquem por que é válida a regra indicada acima. Queremos que eles entendam que denominador maior significa que o inteiro foi dividido em mais partes, logo cada parte resulta menor do que quando tomamos uma fração com denominador menor.
Conclusão:
– Como 2 < 3 e as frações 1/3 e 1/2 têm numerador igual a 1, pode-se concluir que 1/3 <1/2.
– Como 4 < 8 e as frações 1/8 e 1/4 têm numerador igual a 1, pode-se concluir que 1/8 < 1/4.
Mais exemplos (sem as réguas):
Comparar 1/5 e 1/9:
1º – Quais os numeradores? (1 e 1)
2º – Quais são os denominadores? (5 e 9)
3º – Comparar os denominadores. (5 < 9)
4º – Conclusão: Como 5 < 9 e ambos os numeradores são iguais a 1, então 1/9 < 1/5.
Comparar 1/6 e 1/10:
1º – Quais os numeradores? (1 e 1)
2º – Quais são os denominadores? (6 e 10)
3º – Comparar os denominadores. (6 < 10)
4º – Conclusão: Como 6 < 10 e ambos os numeradores são iguais a 1, então 1/10 < 1/6.
Caso 2: NUMERADORES IGUAIS
Em todos os exemplos anteriores, os numeradores eram iguais a 1. Isto é, tomava-se apenas uma régua de cada tipo e, por isso, para comparar as frações dadas, bastava comparar os comprimentos dos dois tipos de réguas dadas ou os denominadores das mesmas. Queremos levar os alunos a concluir que esta mesma regra (comparação de denominadores) é válida sempre que os numeradores forem iguais, mesmo que não sejam 1.
Comparar 2/3 e 2/7:
– Explique que no presente exemplo, para comparar as duas frações, temos que tomar duas réguas de cada e comparar os comprimentos totais. Isto é, deve-se comparar os comprimentos de duas réguas terços e de duas réguas sétimos:

Pela representação acima, é possível perceber que:
2/7 < 2/3
Comparar 5/6 e 5/7:

Comparando os comprimentos das cinco réguas sextos e das outras cinco réguas sétimos, é fácil perceber que:
5/7 < 5/6
– Repita tantos exemplos deste tipo quantos necessários até que os alunos percebam e verbalizem a seguinte regra: mesmo que os numeradores não sejam 1, se eles forem iguais, a fração com menor denominador será maior do que aquela com denominador maior.
3º PASSO: FRAÇÕES COM NUMERADORES E DENOMINADORES DISTINTOS
Exemplo: Comparar 2/3 e 4/5
– Chame a atenção dos alunos para o fato das frações 2/3 e 4/5 não possuírem numeradores ou denominadores iguais.
– Conclua então que não é possível compará-las apenas contando a quantidade de réguas utilizadas para representar cada uma delas (como no caso das frações com denominadores iguais), nem comparar os denominadores a fim de concluir que a fração com menor denominador é a maior dentre as duas (no caso dos numeradores serem iguais).
– Peça-lhes que representem, a partir das réguas, as frações dadas e, em seguida, comparem tais representações.

É fácil perceber que 2/3 < 4/5.
– Questione-os sobre como procederiam se tivessem de comparar frações tais como 24/32 e 18/36.
– Conclua com eles que, nesse caso, apenas a representação através das réguas deixará de ser um método prático de comparação. Daí a necessidade de aprenderem o tópico tema da próxima atividade – frações equivalentes.
3ª atividade: encontrando frações equivalentes
Objetivo: Explorar o conceito de frações equivalentes
Materiais Utilizados: Réguas de frações, ficha de acompanhamento 1.
– Peça aos alunos que representem sobre a régua preta a fração um meio.
– Em seguida que cubram essa fração utilizando réguas de uma única cor e que não seja a amarela.
– Pergunte que réguas utilizaram e quantas delas foram necessárias. Cada aluno (ou grupo) deve dar uma das seguintes respostas: duas réguas quartos, ou três réguas sextos, ou quatro réguas oitavos, ou cinco réguas décimos.
– Explique que, apesar das representações numéricas das frações serem diferentes, elas cobrem o mesmo pedaço do inteiro (metade da régua preta), ou seja, representam a mesma área colorida do inteiro. Logo, são equivalentes.
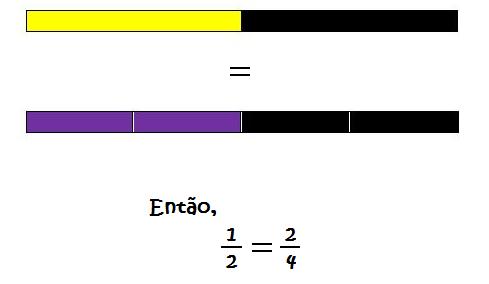
– Compare as representações das frações 1/2 e 2/4 através das réguas.
– Explique que para obter esta equivalência, o que se fez foi dividir a régua dada (meio) em duas partes iguais. Isto é, dobrar a quantidade de réguas tomadas, pois para substituir a régua meio, foram utilizadas duas réguas quartos. Da mesma forma, para representar todo o inteiro com réguas de quartos, usaríamos o dobro da quantidade de réguas que usamos quando o representamos com réguas de meios, afinal cada régua de meio equivale a duas réguas de quarto.
Conclusão: Se uma fração pode ser representada com certa quantidade de réguas de meio, para representá-la com réguas de quarto, necessitaremos do dobro de réguas, já que cada régua de meio equivale a duas réguas de quarto.
Observamos que:

Outro exemplo:
– Peça aos alunos que representem sobre a régua preta a fração quatro sextos.
– Em seguida, oriente-os a encontrarem réguas de uma única cor que cubram as quatro réguas sextos.
– Pergunte que réguas utilizaram e quantas delas foram necessárias. (Espera-se que eles respondam: duas réguas terços.)
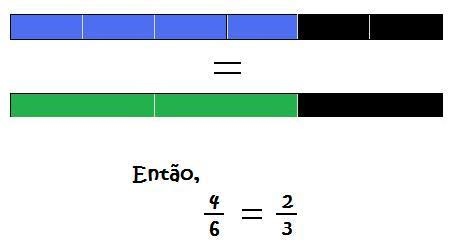
– Comparando as representações das frações 4/6 e 2/3 através das réguas, explique que para cada duas réguas sextos há uma régua terço que ocupa o mesmo espaço. Isto é, agrupando-se as réguas sextos, é possível obter novas réguas: as réguas terços.
Explique que o comprimento dessas novas réguas é o dobro do comprimento da régua sexto, pois as réguas sextos foram agrupadas duas a duas. Isto é, ao invés de ter quatro réguas menores, passa-se a ter apenas duas réguas maiores. E o inteiro, antes dividido em seis partes iguais, fica dividido em três partes, pois é representado por três grupos com duas réguas sextos em cada um.
Numericamente, temos:

– Repita tantos exemplos quantos forem necessários para que os alunos verifiquem que sempre que uma fração tem seu numerador e seu denominador multiplicados (ou divididos) pelo mesmo número, a nova fração obtida é equivalente à inicial.
– Certifique-se de que os alunos entendem que isso ocorre porque, nesses casos, estamos simplesmente “mudando as réguas utilizadas”, mas mantemos a proporção entre o número de réguas que tomamos e o número de réguas necessárias para representar o todo com as réguas em questão.
- Hora de registrar: Após a realização deste passo, recomenda-se que os alunos façam as atividades 4 e 5 da ficha de acompanhamento 1. (A atividade 5 não aborda o tema frações equivalentes. Esses exercícios tratam do significado da fração como parte/todo.)
4ª atividade: simplificando frações (e mais um pouco de comparação)
Objetivos: aplicar as ideias da atividade anterior para trabalhar sobre simplificação de frações e sobre comparação de frações quando que não possuem numeradores iguais nem denominadores iguais.
Agora retome o exemplo sugerido ao final da segunda atividade (comparação de frações), usando o que foi aprendido sobre frações equivalentes para resolvê-lo.
Comparar as frações 24/32 e 18/36:
– Peça que os alunos que encontrem uma fração equivalente à fração 24/32 e com menor denominador (usando o que aprenderam na atividade anterior sobre frações equivalentes).
Observação: Diminuindo-se o denominador, diminui-se também o numerador. Por isso, nenhuma consideração foi feita acima a respeito do numerador.
Relembrando: Na atividade de comparação de frações foi possível perceber que frações com numeradores e denominadores menores são mais fáceis de comparar. Isso porque:
- é possível representá-las através das réguas; ou
- optando pela divisão do numerador pelo denominador, essa conta se torna mais simples com números menores.
– Explique que com isso estamos buscando simplificar a fração 24/32:

Observação: Optou-se aqui pela fração 3/4, pois esta possui o menor denominador possível. Todavia, os alunos podem optar pela fração 6/8, que também possui representação nas réguas.
– Peça aos alunos para, operando de maneira análoga, simplificarem a fração 18/36.
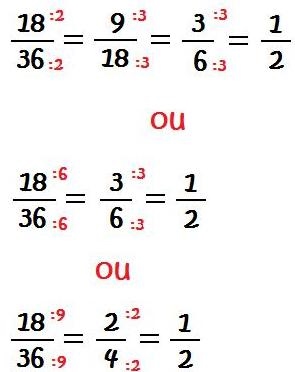
– Observe com os alunos que a fração 24/32 é equivalente à fração 3/4 e a fração 18/36 é equivalente à fração 1/2. Oriente os alunos a representarem com as réguas estas frações.
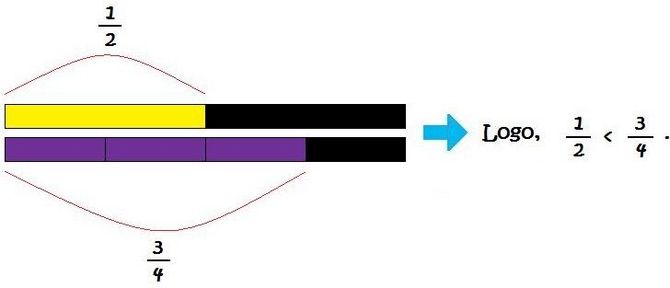
Resumindo:
24/32 = 3/4 e 18/36 = 1/2
1/2 < 3/4
Conclusão:
18/36 < 24/32
– Pergunte aos alunos como eles poderiam ter resolvido sem usar as réguas. Oriente para que eles observem que poderiam ter representado ambas as frações usando o mesmo denominador (24/32 = 3/4 e 18/36 = 1/2 = 2/4), e então comparar apenas os numeradores, como fizemos na segunda atividade.
– Explique que quando encontramos uma fração que não pode mais ser simplificada, isto é, não há como encontrar uma fração equivalente com denominador menor, a fração em questão é chamada de irredutível. Isso ocorre sempre que o único divisor natural em comum do numerador e do denominador é o número 1.
– Desafie os alunos a descobrirem o que tem de especial o número pelo qual devemos dividir o numerador e o denominador para encontrar em um único passo a simplificação à fração irredutível. A resposta é: este número é o mdc (maior divisor comum) do numerador e do denominador.
– Se achar necessário, o professor deve apresentar mais exemplos, tais como:
– comparar as frações 6/15 e 4/16;
– comparar as frações 25/30 e 6/36.
5ª atividade: localizando frações próprias na reta
Objetivo: Vincular a representação das frações próprias através das réguas com a localização do racional correspondente na reta dos números reais.
Materiais Utilizados: Réguas de frações, ficha de atividades 2.
1º PASSO: REPRESENTANDO A UNIDADE
– Peça aos alunos para sobreporem a régua preta à reta do item 1 da folha de atividades 2 e, alinhando o início da régua no zero, marquem o 1 no local onde termina a régua preta.
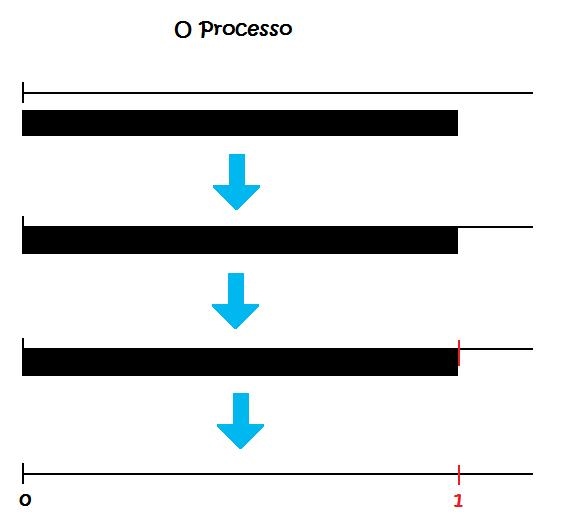
2º PASSO: LOCALIZANDO FRAÇÕES PRÓPRIAS NA RETA
-Peça aos alunos que, ainda no exercício 1 da ficha de atividades 2, sobreponham ao segmento dado uma régua quarto, marcando com um ponto o seu comprimento e escrevendo abaixo desse ponto a fração representada por essa régua (numericamente).
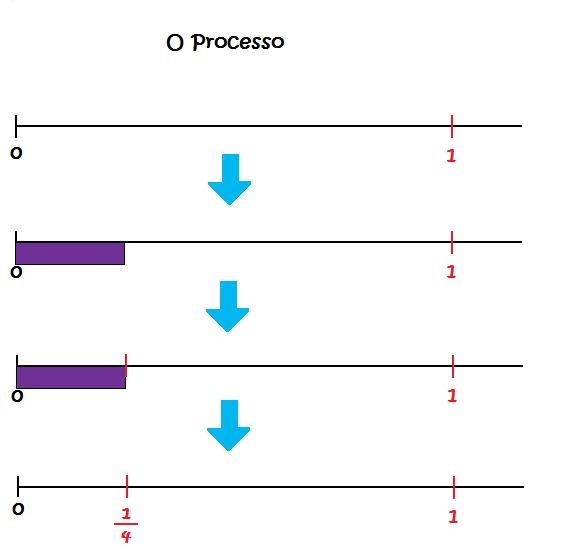
3º PASSO: DIVIDINDO A UNIDADE EM PARTES IGUAIS
– Peça aos alunos que repitam o procedimento até marcarem o ponto quatro quartos. Em seguida, peça-lhes que escrevam a representação numérica das frações obtidas com este procedimento. Nesse ponto é normal que os alunos perguntem porque a fração quatro quartos está localizada no ponto 1 do segmento. Então, pergunte-lhes quantas réguas quartos são necessárias para cobrir a régua preta (o inteiro). (Espera-se que eles respondam: quatro réguas.)

– Chame a atenção dos alunos para o fato de quatro réguas quartos ocuparem o mesmo espaço que uma régua preta. Assim, a fração 4/4 é equivalente a um inteiro.
4º PASSO: LOCALIZANDO FRAÇÕES PRÓPRIAS NA RETA SEM O AUXÍLIO DAS RÉGUAS
– Peça aos alunos que, no exercício 2 da ficha de atividades 2, marquem a unidade (usando a régua preta) no primeiro segmento. Em seguida, peça-lhes que dividam o comprimento obtido em três partes iguais e localizem a fração 2/3.
– Os alunos devem repetir o mesmo procedimento de divisão em 3 partes para os outros segmentos menores e, em cada um, devem localizar a fração 2/3.
– Pergunte-lhes se notaram alguma diferença ao localizarem a mesma fração em segmentos de comprimentos diferentes.
– Conclua que é possível dividir qualquer segmento em partes iguais, independentemente de seu comprimento, e que o tamanho que corresponde à fração 2/3 em um segmento depende do comprimento do próprio segmento.
6ª atividade: localizando frações impróprias na reta
Objetivo: Espera-se, ao final desta atividade, que os alunos sejam capazes de identificar a localização de frações impróprias na reta numérica.
Materiais Utilizados: Réguas de frações, ficha de atividades 3.
1º PASSO: REPRESENTANDO FRAÇÕES IMPRÓPRIAS
– Reagrupe os alunos de forma que cada grupo disponha de dois kits de réguas.
– Peça que tomem seis réguas vermelhas e, lembrando que cada uma delas representa um quinto, pergunte qual fração corresponde às seis réguas.

– Peça que representem numericamente esta fração e que escrevam-na por extenso, assim como foi feito com a frações própria 2/5, no 5º passo da 1ª atividade. O objetivo é reforçar a ideia de que o numerador está associado à a quantidade de réguas tomadas e que o denominador está associado ao nome dessas réguas.

- Hora de registrar: Após a realização deste passo, recomenda-se que os alunos façam a atividade 6 da ficha de acompanhamento 1.
2º PASSO: LOCALIZANDO FRAÇÕES IMPRÓPRIAS NA RETA
– No passo anterior, ao compararem o comprimento das seis réguas vermelhas (quintos) alinhadas e o comprimento da régua preta, os alunos devem ter notado que as réguas vermelhas excedem a preta. Logo, a fração seis quintos é maior que um inteiro. Isto é:
6/5 > 1
– Explique que, nesse caso, como a fração é maior do que o inteiro, para representá-la, os alunos vão precisar de mais uma régua preta (inteiro).

- Hora de registrar: O professor deve solicitar que os alunos marquem no item 1 da ficha de acompanhamento 3 o ponto onde deve se localizar a fração seis quintos. É importante chamar a atenção dos alunos para o fato das frações impróprias serem sempre maiores que a unidade.
– Antes de localizar a fração seis quintos na reta apresentada na atividade 1 da ficha de acompanhamento 3, os alunos já devem ser capazes de perceber que a mesma estará após o número 1. Caso haja ainda alguma dúvida em relação a isso, o professor deve retomar a ideia da atividade 1 da ficha de acompanhamento 2, onde a régua preta, que representa o inteiro, tem o mesmo comprimento do segmento [0,1]. Como, nesse exemplo, temos duas réguas pretas, tem-se também um comprimento maior do que 1.
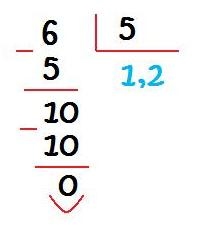
– Para precisar esse comprimento, podemos lançar mão de outro recurso além das réguas de frações: o algoritmo da divisão. O professor deve explicar aos alunos que a fração pode ser entendida como um quociente e que esse quociente, resultado da divisão do numerador pelo denominador, é a representação decimal da fração dada que, por sua vez, pode ser encontrada na reta numérica.
- Hora de registrar: Após a realização deste passo, recomenda-se que os alunos façam as atividades 7 e 8 da ficha de acompanhamento 1.
3º PASSO – PRATICANDO UM POUCO MAIS
– Utilizando réguas de outras cores, repita este procedimento para outras frações impróprias, como cinco terços, três meios, sete quintos, dez oitavos, oito sextos, cinco meios, onze quartos, quinze terços etc.
- Hora de registrar: O professor deve solicitar que os alunos localizem cada fração citada acima nas atividades 1 e 2 da ficha de acompanhamento 3. (É importante localizar as mesmas frações também na atividade 2 para que os alunos sejam capazes de perceber que, independentemente da escala utilizada na representação da reta numérica, uma determinada fração estará sempre localizada entre os mesmos dois inteiros.)
ARQUIVOS PARA DOWNLOAD
Ficha de Acompanhamento 1
Ficha de Acompanhamento 2
Ficha de Acompanhamento 3
Guia para produção de réguas com EVA ou canudos

