Soma e subtração de frações usando canudos ou réguas de frações

Helena Calvo, Liliane Branco e Anne Michelle Dysman

Esta atividade destina-se ao ensino das operações de adição e subtração com frações. Tratamos inicialmente das frações com denominadores iguais e, em seguida, das frações com denominadores distintos. Utilizaremos como recurso as réguas de frações (indicamos como produzir uma versão de baixo custo). Caso a turma ainda não conheça este material, sugerimos que antes sejam realizadas as atividades iniciais do Módulo Instrucional Introdução às Frações com Réguas de Frações para que os alunos se familiarizem com ele.

Utilizaremos as réguas de frações como recurso pedagógico. Algumas escolas possuem este material, o qual também pode ser adquirido em lojas que comercializam brinquedos pedagógicos. O ideal para o desenvolvimento do trabalho é que cada aluno possa utilizar um jogo de réguas. Como nem sempre as escolas ou os alunos dispõem de recursos financeiros para a aquisição deste material, fornecemos no plano de aula “Frações: uma introdução com canudos ou réguas de frações” instruções para a produção do mesmo.

Sugerimos que os alunos sejam divididos em duplas para a realização do trabalho.

Materiais Utilizados

– réguas de frações (um kit por aluno ou por dupla – instruções para preparação de uma versão de baixo custo são encontradas no módulo instrucional Frações: uma introdução com réguas de frações);

– ficha de acompanhamento (uma por aluno).

Descrição do material (réguas de frações)

A descrição do material encontra-se no módulo instrucional “Frações: uma introdução com réguas de frações“.

Etapas do Trabalho

Recomendamos que antes que seja realizado o trabalho proposto neste módulo, o professor realize com seus alunos as atividades do módulo instrucional “Frações: uma introdução com réguas de frações“.

1ª atividade: Soma e subtração de frações com denominadores iguais;
2ª atividade: Soma e subtração de frações com denominadores distintos.

Atividades

1ª atividade: Soma e subtração de frações com denominadores iguais

Objetivos: Levar os alunos a perceberem que a soma e a subtração de frações com mesmo denominador se reduzem, respectivamente, à soma e à subtração da quantidade de réguas tomadas e, portanto, à soma e à subtração de números naturais.

Materiais Utilizados: réguas de frações e ficha de atividades

1º PASSO – EXEMPLOS

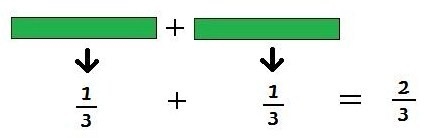
Exemplo 1: 1/3 + 1/3

Peça aos alunos que sobreponham à régua preta duas réguas terços e, em seguida, questione-os sobre que fração da unidade estas duas réguas juntas representam.

(Pelo trabalho desenvolvido até agora, espera-se que eles respondam dois terços.)

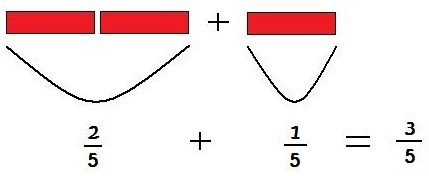
Exemplo 2: 2/5 + 1/5

Exemplo 3: 2/4 – 1/4

Peça aos alunos que peguem duas réguas quartos e sobreponham à régua preta.

Após analisarem o resultado, solicite que retirem uma régua das réguas.

Chame a atenção dos alunos para o fato da subtração de frações com denominadores iguais ser feita do mesmo modo que a adição, isto é, mantendo-se o denominador e subtraindo-se apenas os numeradores.

Para melhor compreensão por parte dos alunos, recomenda-se a realização de mais exemplos, tais como:

5/4 + 2/4 = 7/4

1/5 + 3/5 = 4/5

3/5 – 1/5 = 2/5

6/7 – 2/7 = 4/7

Hora de registrar: Ao final deste passo, peça aos alunos que façam os exercícios 1 e 2 da ficha de atividades.

2º PASSO – SIMPLIFICAÇÃO

Exemplo 1: 1/2 + 1/2

Ao somar ou subtrair algumas frações pode-se obter como resultado uma fração na qual o numerador e o denominador são iguais.

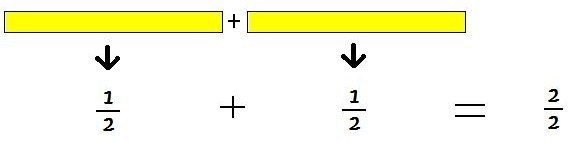
Note que a fração 2/2 pode ser simplificada.

Observação:

Consultar a 2ª atividade do módulo instrucional Frações: uma introdução com réguas de frações, que trata de frações equivalentes e simplificação.

Para simplificar esta fração, primeiramente, deve-se buscar uma fração equivalente a ela.

Chame a atenção dos alunos para a ideia desenvolvida no módulo anterior, de que simplificar significa agrupar as réguas para obter uma nova régua.

Peça aos alunos que agrupem as duas réguas “meios”, formando assim uma nova régua cujo comprimento é o dobro do comprimento de uma régua “meio”.

Em seguida, peça a eles que procurem no kit uma régua de mesmo tamanho que a nova régua obtida.

(Nesse caso, a régua encontrada no kit será a preta, que representa o inteiro.)

Chame a atenção deles para o fato da unidade poder ser representada pelo número 1 ou pela fração 1/1.

Numericamente,

Isso acontece porque o numerador e o denominador da fração 2/2 têm divisores comuns. Tomando-se o maior desses divisores, isto é, o maior divisor comum (mdc), e dividindo-se ambos os termos por ele, obtém-se uma fração equivalente à fração dada, em sua forma simplificada.

Nesse exemplo o mdc é 2.

Exemplo 2: 3/4 + 3/4

Nesse caso, deve-se dividir o numerador e o denominador pelo seu maior divisor comum (mdc).

Como o mdc(6,4) = 2,

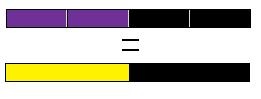
Exemplo 3: 3/4 – 1/4 = 2/4

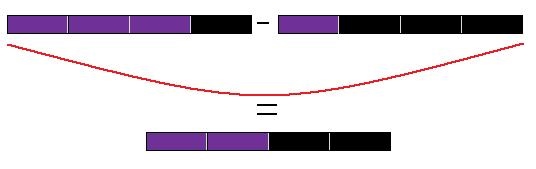
Peça aos alunos que agrupem as duas réguas “quartos”, formando assim uma nova régua cujo comprimento é o dobro do comprimento de uma régua “quarto”.

Em seguida, peça a eles que procurem no kit uma régua de mesmo tamanho que a nova régua obtida.

Nesse caso, a régua encontrada no kit será a amarela, que representa 1/2 do inteiro.

Nesse caso, assim como na adição, para obter-se a equivalência 2/4 = 1/2, deve-se dividir o numerador e o denominador pelo seu maior divisor comum (mdc).

Como o mdc(2,4) = 2, então

Para melhor compreensão por parte dos alunos, recomenda-se a realização de mais alguns exemplos, tais como:

1/3 + 2/3 = 3/3 = 1

1/4+ 2/4 = 3/4

4/6 – 2/6 = 2/6 = 1/3

10/8 – 2/8 = 8/8 = 1

Hora de registrar: Ao final deste passo, peça aos alunos que façam o exercício 3 da ficha de atividades.

2ª atividade: Soma e subtração de frações com denominadores distintos

Objetivo: Levar os alunos a compreenderem a adição e a subtração de frações com denominadores distintos utilizando o conceito de frações equivalentes.

Materiais Utilizados: réguas de frações e ficha de atividades

1º PASSO: EXEMPLO

Exemplo 1: 1/2 + 1/3

Peça aos alunos que peguem uma régua meio e uma régua terço e sobreponham à régua preta.

Pergunte a eles que fração da unidade foi coberta pelas duas réguas.

Para responder a esta pergunta o professor deve chamar a atenção para a diferença no comprimento das réguas. Isto significa que as frações têm denominadores diferentes.

2º PASSO: ENCONTRANDO FRAÇÕES EQUIVALENTES

Para somar estas frações faz-se necessário procurar réguas iguais que cubram totalmente tanto a régua meio quanto a régua terço. Neste caso, as réguas “sextos”.

A partir do esquema acima, conclua com seus alunos que eles encontraram frações equivalentes às frações 1/2 e 1/3 com um mesmo denominador. Isto é, a fração 1/2 é equivalente à fração 3/6 e a fração 1/3 é equivalente è fração 2/6.

3º PASSO: CONCLUINDO O EXEMPLO

Pelo passo anterior,

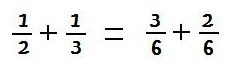
Chame a atenção dos alunos para o fato de terem transformado uma soma de frações de denominadores distintos numa soma de frações com mesmo denominador. Assim, pela atividade anterior,

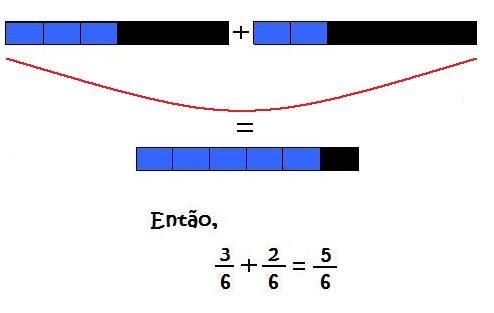
Daí, pode-se concluir que:

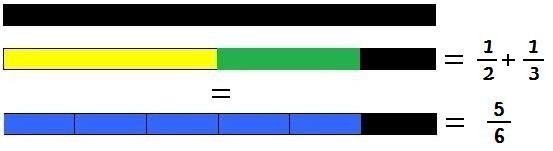
4º PASSO: EXEMPLO

Exemplo 2: 1/2 – 1/3

Peça aos alunos que peguem uma régua meio e a sobreponham ao inteiro (régua preta). Em seguida, que sobreponham a esta régua uma régua terço.

Desse modo:

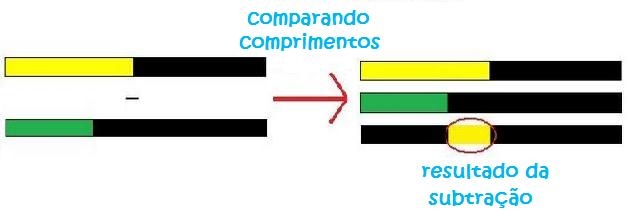
Pergunte a eles se são capazes de dizer que fração do inteiro representa esse pedacinho que sobrou da régua amarela.

(Nesse momento, eles já devem ser capazes de perceber que terão de encontrar uma fração equivalente a 1/2 e uma fração equivalente a 1/3 que possuam o mesmo denominador.)

5º PASSO: ENCONTRANDO FRAÇÕES EQUIVALENTES

Peça a eles que procurem réguas iguais que cubram totalmente tanto a régua meio quanto a régua terço.

Como eles já descobriram na atividade de adição que a régua em questão é “sexto”, temos que:

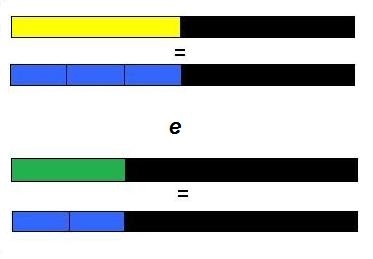
Daí,

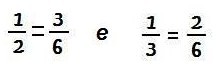
Conclua com os alunos que 3/6 e 2/6 são frações equivalentes, respectivamente, às frações 1/2 e 1/3.

6º PASSO: CONCLUINDO O EXEMPLO

Pelo exemplo anterior,

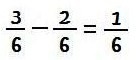
Agora peça a eles que comparem o pedacinho da régua amarela que sobrou com o comprimento de uma régua sexto.

Pergunte a eles o que eles puderam observar.

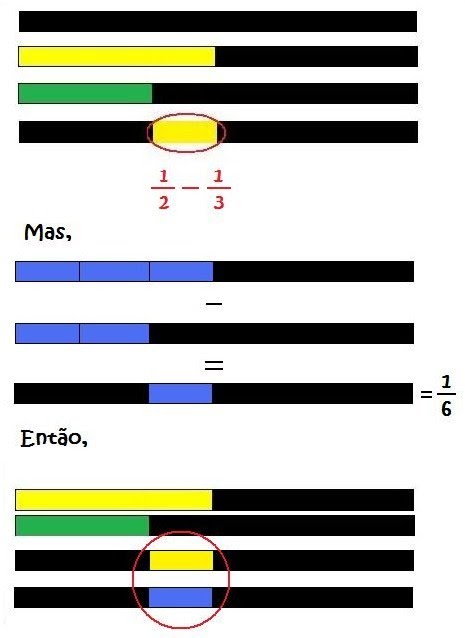
Então,

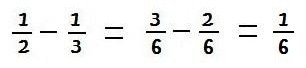
Recomenda-se repetir o processo para outras frações, tais como:

2/4 + 2/5 = 10/20 + 8/20 = 18/20 = 9/10

1/2 + 1/4 = 2/4 + 1/4 = 3/4

3/5 – 1/2 = 6/10 – 5/10 = 1/10

7/8 – 1/4 = 7/8 – 2/8 = 5/8

Hora de registrar: Ao final deste passo, peça aos alunos que façam os exercícios 4 e 5 da ficha de atividades.