Entendendo Múltiplos e MMC

Jéssica Rama, Marcella Candido e Anne Michelle Dysman

O objetivo desta atividade é promover a aprendizagem de múltiplos dos números naturais e do MMC (mínimo múltiplo comum) de forma significativa. Através de materiais concretos (fichas e tabuleiro) trabalhamos a fatoração em primos de números naturais conduzindo o aluno a construir a ideia de decomposição do número em fatores primos. Este módulo instrucional dá sequência ao módulo “Números primos e fatoração com a escala Cuisenaire”, o qual recomendamos que seja aplicado com os alunos antes deste, pois este depende do conhecimento prévio da fatoração em primos.

A atividade poderá ser realizada em grupos de no máximo três alunos, mas cada aluno deverá registrar individualmente suas observações em uma ficha de acompanhamento.

Objetivos

Promover a aprendizagem de múltiplos dos números naturais e do MMC (mínimo múltiplo comum) de forma significativa.

Materiais utilizados

– Kit MMC e MDC composto por tabuleiro e fichas (a ser produzido de acordo com o Guia para Produção do Kit MMC e MDC). Abaixo encontram-se imagens que ilustram este kit.

– Tabuada

– Fichas de acompanhamento fornecidas neste plano.

Etapas do trabalho

É necessário que o aluno saiba fatorar números naturais em primos para ter boa aprendizagem do conteúdo aqui ministrado. Caso os alunos tenham dificuldades com a fatoração recomendamos que o professor utilize o Módulo Instrucional Números Primos e Fatoração com a Escala Cuisenaire para ministrar assunto antes de efetuar o trabalho aqui proposto.

1ª atividade: Descobrindo múltiplos através da fatoração em números primos

2ª atividade: Calculando MMC através da fatoração em números primos

3ª atividade: Relacionando a atividade com o algoritmo da fatoração simultânea

Atividades

1ª atividade: Descobrindo múltiplos através da fatoração em números primos

Objetivos: Rever fatoração em primos e trabalhar sobre o conceito de múltiplos dos números naturais relacionando-o à fatoração em primos.

Materiais: Tabuada e ficha de acompanhamento 1.

1º PASSO – RELEMBRANDO OS CONCEITOS DE MÚLTIPLOS, DIVISORES, PRIMOS E FATORAÇÃO.

– Relembramos para os alunos a definição de múltiplos: Os múltiplos de um número natural são os números que obtemos quando multiplicamos este natural por qualquer outro. Por exemplo, para encontrarmos os múltiplos de 7, devemos multiplicá-lo pela sucessão dos números naturais: 7×0, 7×1, 7×2, 7×3, 7×4, 7×5, e assim por diante.

Sendo assim, alguns dos múltiplos de 7 são: 0, 7, 14, 21, 28, 35,…

– Relembramos também o conceito de divisor de forma associada a de múltiplo: se 28 é múltiplo de 7, então 7 é divisor de 28. Utilize vários exemplos para se certificar que os alunos compreendem bem os conceitos de múltiplos e divisores.

– Fazemos algumas perguntas aos alunos sobre primos e fatoração: “o que são os números primos?”, “o que é a fatoração em números primos de um número natural?”, “como fatoramos um número natural?” Esses conceitos serão fundamentais para a realização das atividades deste módulo instrucional.

– Após responderem à primeira pergunta, liste os primeiros nove números primos junto com os alunos (2, 3, 5, 7, 11, 13, 17, 19 e 23). Anote estes números em um canto do quadro para serem usados posteriormente.

– Após responderem às outras duas perguntas, fazemos junto com os alunos alguma fatoração. Podemos, por exemplo, fatorar o número 24, que utilizaremos mais adiante.

2º PASSO – OBSERVAÇÃO DE MÚLTIPLOS E DIVISORES PELA TABUADA

– Vamos mostrar aos alunos como podemos identificar múltiplos com o uso da tabuada:

As tabuadas de multiplicação dos números de zero a dez representam os onze primeiros múltiplos destes números. Vejamos na tabuada a seguir alguns dos múltiplos do número 6:

Tabuada de Multiplicação do Número 6

6 . 0 = 0

6 . 1 = 6

6 . 2 = 12

6 . 3 = 18

6 . 4 = 24

6 . 5 = 30

6 . 6 = 36

6 . 7 = 42

6 . 8 = 48

6 . 9 = 54

6 . 10 = 60

Recorrendo à tabuada acima vemos que 12 é múltiplo de 6 (e portanto, 6 é divisor de 12), pois 12 = 2 x 6. Para formarmos o número 12, somamos múltiplas vezes ao número 6 (mas precisamente, 2 vezes):

6 + 6 = 12

Observamos, contudo, que 72 é múltiplo de 6, pois 72 = 6 x 12, mas que isto não pode ser verificado imediatamente na tabuada usual, pois ela só nos dá os 11 primeiros múltiplos de cada número. Então seria bom ter outro método prático para verificar quando um número é múltiplo de outro.

Vale lembrar aos alunos que o conjunto dos múltiplos de um número natural é infinito, pois a multiplicação de um número natural, por um outro número natural irá produzir um dos seus múltiplos e, como sabemos, o conjunto dos números naturais é um conjunto infinito.

Hora de registrar: Ao final deste passo, peça aos alunos que respondam ao exercício 1 da ficha de acompanhamento 1.

3º PASSO – FATORAÇÃO E MÚLTIPLOS

No módulo instrucional Números Primos e Fatoração com a Escala Cuisenaire ensinamos aos alunos como realizar a fatoração em primos de um número natural. Agora vamos utilizar esta fatoração para encontrar todos os divisores de um natural dado (e, portanto, poderemos assim descobrir de quais outros números ele é múltiplo). Por exemplo, observe a fatoração do número 24:

Vemos que o 24 tem como divisores 2,3,4,6,8, e 12, pois os mesmos podem ser obtidos como produto de fatores primos de 24. Isto significa que 24 é múltiplo de 2,3,4,6,8, e 12.

Hora de registrar: No exercício 2 da ficha de acompanhamento 1, os alunos deverão fatorar os número dados em cada retângulo, e em seguida responder os itens a,b,c e d de acordo com proposta descrita acima.

Com esse exercício esperamos que o aluno perceba que pela fatoração em números primos de um número n, podemos descobrir todos os seus divisores naturais, o que significa que poderemos saber de quais números naturais n é múltiplo. Desta forma podemos identificar múltiplos sem usar a tabuada. Por exemplo: O número 36 é múltiplo do 18, (pois a fatoração do 36 é 3x3x2x3, e o 18=3x2x3). Observe que seria difícil verificar este fato diretamente pela tabuada, já que geralmente o aluno só aprende a tabuada do número 1 ao 10.

Hora de registrar: No exercício 3 da ficha de acompanhamento 1, os alunos deverão observar a fatoração do número 6120 e responder às perguntas lá formuladas.

2ª atividade: Calculando MMC através da fatoração em números primos

Objetivos: Desenvolver o conceito de mínimo múltiplo comum de dois números através da fatoração destes em número primos. Promover a aprendizagem significativa de MMC utilizando para isso recursos concretos.

Materiais: Kit MMC e MDC e ficha de acompanhamento 2.

Ao fatorar um número em primos o que fazemos é efetuar uma decomposição deste número em certos fatores especiais (números primos) que podem ser considerados como “blocos de construção” que nos permitem compor qualquer natural. O kit que utilizamos neste módulo instrucional se propõe a dar concretude a estes “blocos de construção” e com isso facilitar a aprendizagem significativa de múltiplos, divisores, mmc e mdc (divisores e mdc serão trabalhados no próximo módulo instrucional).

1º PASSO – EXPLORANDO O MATERIAL

– Deixe que os alunos que manipulem as fichas do material recebido e perguntem o que observam sobre elas. Eles devem perceber que as fichas circulares representam números primos. Pode ser que percebam também que os números nas fichas retangulares não são primos.

– Peça para separarem as fichas circulares das retangulares, formando dois grupos de fichas.

– Desenhe na lousa o tabuleiro.

2º PASSO – ENCONTRANDO O MMC ATRAVÉS DA OBSERVAÇÃO DAS FATORAÇÕES

– Escolha duas fichas retangulares e peça para que os alunos as coloquem sobre o tabuleiro no espaço retangular. Começaremos com 12 e 15.

– Utilizando as fichas circulares que contém os números primos, explique que eles deverão reescrever esses dois números na forma fatorada, colocando as fichas utilizadas sobre o tabuleiro. Como na figura abaixo:

– Desafie os alunos a buscarem o menor conjunto de fichas circulares que nos permita representar tanto a fatoração do primeiro número quanto a do segundo (uma de cada vez). Por exemplo, no caso acima, para fatorar 12 precisamos de duas fichas 2 e uma ficha 3. Já para fatorar 15 precisamos de uma ficha 3 e uma 5. Então se tivermos duas fichas 2, uma 3 e uma 5 seremos capazes de escrever tanto a fatoração do 12 quanto a do 15 (uma de cada vez). Este é o menor conjunto de fichas que nos permitirá fazer as duas representações.

– Após obter junto com os alunos a conclusão acima, utilize as fichas circulares selecionadas para completar a última linha do tabuleiro e procure uma ficha retangular que possa ser utilizada como resultado da multiplicação registrada. Ficaremos com:

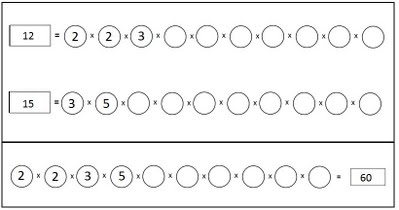
Observe que, no exemplo acima, embora a ficha 3 apareça tanto na fatoração do 12 quanto na do 15, não é preciso repeti-la, já que a mesma aparece apenas uma vez em cada uma das fatorações. Esta ficha é comum às duas fatorações.

– Enfatize que o número obtido (60) é múltiplo tanto de 12 quanto de 15 (considerando a relação entre múltiplos e fatoração trabalhada no segundo passo da atividade 1).

– Proponha aos alunos que tentem, retirando alguma das fichas circulares selecionadas, obter um outro número que não seja zero e que também seja múltiplo do 12 e do 15. Faça com que percebam a impossibilidade de ter sucesso nesta busca.

– Conclua que 60 não apenas é múltiplo de 12 e 15, como também é o menor número que é múltiplo comum a 12 e 15.

– Defina o MMC a partir da atividade desenvolvida:

“O menor múltiplo comum (MMC) de dois números naturais é o menor número natural não nulo que é múltiplo dos dois números dados”

Logo, o MMC de 12 e 15 é 60. Denotamos:

MMC(12,15) = 60

– Peça aos alunos que realizem esta atividade para os exemplos a seguir. Cada um deles deve ser registrado através do preenchimento de um tabuleiro na ficha de acompanhamento 2.

Hora de registrar: Cada um dos exemplos abaixo deve ser registrado em um tabuleiro da ficha de acompanhamento 2.

1) MMC(4,6)

4 = 2 x 2

6 = 2 x 3

A solução esperada é: 2 x 2 x 3 = 12

2) MMC(6,10)

6 = 2×3

10 = 2×5

A solução esperada é: 2 x 3 x 5 = 30

3) MMC(8,9)

8 = 2x2x2

9 = 3×3

A solução esperada é: 2 x 2 x 2 x 3 x 3 = 72

– Após o exemplo acima pergunte aos alunos se observaram algo de especial com este caso. Devem reparar que 8 e 9 não possuem nenhum fator primo em comum. Nesse caso é fácil observar que o MMC deve ser o produto dos dois números (já que todas as fichas circulares usadas para compor os dois números são necessárias para representar o MMC).

– Defina primos entre si e enuncie a propriedade observada sobre o MMC de primos entre si:

Dois números naturais que não possuem nenhum fator primo em comum são chamados primos entre si. O MMC de dois números primos entre si é o produto destes números.

– Outros exemplos a serem trabalhados pelos alunos:

4) MMC(2,7)

2 = 2

7 = 7

A solução esperada é: 2 x 7 = 14

Observar que 2 e 7 são primos entre si.

5) MMC(5,10)

5 = 5

10 = 2 x 5

A solução esperada é: 2 x 5 =10

Após este exemplo, o professor deve levar os alunos a observarem que sempre que um número natural é múltiplo de outro, o número maior é o MMC dos dois.

O professor pode propor outros exemplos caso note que os alunos não estão dominando a atividade proposta.

3ª atividade: Calculando MMC através da fatoração simultânea em primos

Objetivo: Ensinar de forma significativa o algoritmo da fatoração simultânea relacionando-o com o método para encontrar MMC visto nas atividades anteriores. Uma vez que nos certifiquemos que os alunos compreenderam o conceito de MMC e o método usado nas atividades anteriores para obtê-lo, vamos relacionar este procedimento já visto com o algoritmo da fatoração simultânea, processo usual para encontrar o MMC de dois naturais dados. Vamos trabalhar ao mesmo tempo com o tabuleiro e as fichas e com o algoritmo da fatoração para garantir que a relação entre os dois métodos fique clara. Seguimos com um exemplo que mostra como este trabalho deve ser realizado. Vamos calcular o MMC de 12 e 15. A ilustração abaixo mostra o tabuleiro e o primeiro passo do algoritmo:

Podemos ver sublinhados em azul e em verde os resultados após a primeira divisão, tanto no algoritmo quanto no tabuleiro. Os números que abaixo aparecem riscados no tabuleiro devem ter suas fichas retiradas do tabuleiro à medida que as divisões vão sendo efetuadas; na lousa o professor deve cortá-los como acima. Seguem as etapas que dão continuidade ao trabalho:

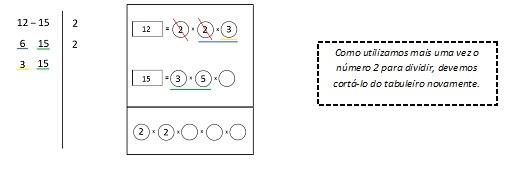
Hora de registrar: Agora seguem outros exemplos a serem desenvolvidos pelos alunos, mas desta vez usando a ficha de acompanhamento 3 e trabalhando simultaneamente com o kit e com o algoritmo da fatoração simultânea:

6) MMC (6,35)

6 = 2 x 3

35 = 5 x 7

A solução esperada é: 2 x 3 x 5 x 7 = 210

Observar que 6 e 35 são primos entre si.

7) MMC(4, 22)

4 = 2 x 2

22 = 2 x 11

A solução esperada é: 2 x 2 x 11 = 44

8) MMC(15,25)

15 = 3 X 5

25 = 5 X 5