Jéssica Rama, Marcella Candido e Anne Michelle Dysman
O ensino de MDC (menor divisor comum entre dois números naturais) frequentemente reduz-se ao método de cálculo de MDC conhecido como algoritmo de Euclides. Este método é bastante prático pois permite que se encontre o MDC em poucos passos e sem a necessidade de fatorar os números. Contudo, trata-se de um método que não põe em evidência o significado do MDC e que geralmente é simplesmente memorizado pelos alunos sem maior compreensão do que estão fazendo. Assim, mais uma vez os alunos repetem um método sem entender por que funciona e, mais ainda, muitas vezes, nem mesmo entendem realmente o que é o MDC. Por outro lado, encontrar o MDC por fatoração é algo que não traz muita dificuldade e que, se trabalhado adequadamente, promove também a compreensão do próprio significado do máximo divisor comum. Esta é a razão pela qual nesta atividade optamos pela fatoração para trabalhar o conceito de MDC e não abordamos o algoritmo de Euclides. Caso o professor deseje trabalhar tal algoritmo, sugerimos que o faça após desenvolver atividades com fatoração e MDC como as propostas neste módulo e que aborde o algoritmo de Euclides por uma perspectiva investigativa (uma vez que já saibam o que é o MDC e como este é calculado por fatoração, tente levá-los a investigar porque funciona o algoritmo de Euclides). Esta proposta para trabalhar o algoritmo de Euclides pode ser especialmente interessante para alunos que apresentam facilidade para atividades que exigem raciocínio matemático formal.
O objetivo deste módulo instrucional é promover a aprendizagem de múltiplos dos números naturais e do MMC (mínimo múltiplo comum) de forma significativa. Através de materiais concretos (fichas e tabuleiro) trabalhamos a fatoração em primos de números naturais conduzindo o aluno a construir a ideia de decomposição do número em fatores primos. Este módulo instrucional dá sequência ao módulo “Números primos e fatoração com a escala Cuisenaire”, o qual recomendamos que seja aplicado com os alunos antes deste, pois este depende do conhecimento prévio da fatoração em primos.
A atividade poderá ser realizada em grupos de no máximo três alunos, mas cada aluno deverá registrar individualmente suas observações nas fichas de acompanhamento.
Objetivos
Promover a aprendizagem de divisores dos números naturais e do MDC (máximo divisor comum) de forma significativa.
Materiais utilizados
– Kit MMC e MDC composto por tabuleiro e fichas (a ser produzido de acordo com o Guia para Produção do Kit MMC e MDC). Abaixo encontram-se imagens que ilustram este kit.
– Fichas de acompanhamento fornecidas neste plano.


Etapas do trabalho
É necessário que o aluno saiba fatorar números naturais em primos para ter boa aprendizagem do conteúdo aqui ministrado. Caso os alunos tenham dificuldades com a fatoração recomendamos que o professor utilize o Módulo Instrucional Números Primos e Fatoração com a Escala Cuisenaire para ministrar assunto antes de efetuar o trabalho aqui proposto. Recomendamos também que sejam desenvolvidas as atividades do módulo instrucional Entendendo Múltiplos e MMC como preparação para esta atividade. Se essa recomendação for seguida, a primeira atividade deste módulo poderá ser realizada de forma muito mais sucinta, visto que é praticamente idêntica à primeira atividade do módulo sobre MMC.
1ª atividade: Descobrindo divisores através da fatoração em números primos;
2ª atividade: Calculando MDC através da fatoração em números primos.
Atividades
1ª atividade: Descobrindo divisores através da fatoração em números primos
Objetivos: Rever fatoração em primos e trabalhar sobre o conceito de divisores dos números naturais relacionando-o à fatoração em primos.
Materiais: Canetas coloridas (tipo hidrocor) ou lápis de cor ou de cera colorido, ficha de acompanhamento 1.
1º PASSO – RELEMBRANDO OS CONCEITOS DE MÚLTIPLOS, DIVISORES, PRIMOS E FATORAÇÃO.
– Relembramos para os alunos a definição de divisores: Os divisores de um número natural são aqueles números pelos quais podemos dividir o número dado obtendo resto zero nesta operação.
Por exemplo, 4 é divisor de 12, pois ao dividirmos 12 por quatro obtemos resto zero (sendo 3 o resultado da divisão).
É importante lembrar que um número natural tem uma quantidade finita de divisores. Por exemplo, o número 6 poderá ter no máximo 6 divisores, pois trabalhando no conjunto dos números naturais não podemos dividir 6 por um número maior do que ele.
2º PASSO – FATORAÇÃO E DIVISORES
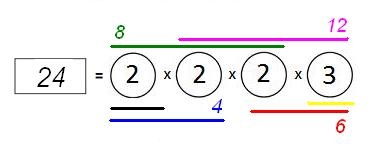
Através da fatoração de um número em primos é possível descobrir quais os divisores do número dado. Por exemplo, observe a fatoração do número 12:
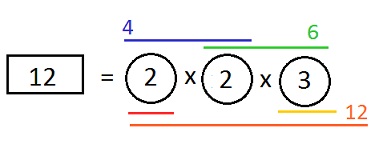
É importante ressaltar aos alunos que todo número natural é divisível por 1 e por ele mesmo.
Portanto, seus os divisores do número 12 são: 1, 2, 3, 4,6 e 12.
Abaixo temos outro exemplo, com o número 30.
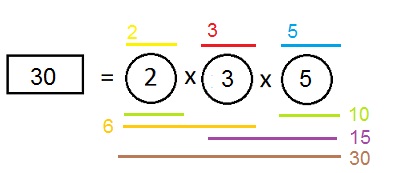
Seus divisores são 1, 2, 3, 5, 6, 10, 15 e 30.
Reproduza este exemplo com seus alunos e os oriente para que resolvam a questão 1 da ficha de acompanhamento 1 seguindo este modelo. Em seguida devem resolver as outras questões da ficha 1.
- Hora de registrar: Ficha de acompanhamento 1.
2ª atividade: Calculando MDC através da fatoração em números primos
Objetivos: Desenvolver o conceito de máximo divisor comum de dois números através da fatoração destes em número primos. Promover a aprendizagem significativa de MDC utilizando para isso recursos concretos.
Materiais: Kit MMC e MDC e ficha de acompanhamento 2.
Ao fatorar um número em primos o que fazemos é efetuar uma decomposição deste número em certos fatores especiais (números primos) que podem ser considerados como “blocos de construção” que nos permitem compor qualquer natural. O kit que utilizamos neste módulo instrucional se propõe a dar concretude a estes “blocos de construção” e com isso facilitar a aprendizagem significativa de múltiplos, divisores, mmc e mdc.
1º PASSO – EXPLORANDO O MATERIAL
– Deixe que os alunos que manipulem as fichas do material recebido e perguntem o que observam sobre elas. Eles devem perceber que as fichas circulares representam números primos. Pode ser que percebam também que os números nas fichas retangulares não são primos. (Caso o professor já tenha trabalhado sobre o módulo instrucional “Entendendo Múltiplos e MMC” com seus alunos, este passo pode ser pulado.)
– Peça para separarem as fichas circulares das retangulares, formando dois grupos de fichas.
– Desenhe na lousa o tabuleiro.
2º PASSO – ENCONTRANDO O MDC ATRAVÉS DA OBSERVAÇÃO DAS FATORAÇÕES EM PRIMOS
– Escolha duas fichas retangulares e peça para que os alunos as coloquem sobre o tabuleiro no espaço retangular. Começaremos com 180 e 140.
– Utilizando as fichas circulares que contém os números primos, explique que eles deverão reescrever esses dois números na forma fatorada, colocando as fichas circulares utilizadas sobre o tabuleiro. Como na figura abaixo:

– Desafie os alunos a buscarem o maior conjunto de fichas circulares que estão presentes tanto na fatoração do primeiro número quanto na do segundo. Por exemplo, no caso acima, para fatorar 180 usamos duas fichas de 2, duas fichas de 3 e uma ficha de 5. Já para fatorar 140 precisamos de duas fichas de 2, uma de 5 e uma de 7. Então o maior conjunto de fichas que aparece tanto em uma quanto na outra fatoração contém duas fichas de 2 e uma de 5 (já que as fichas 3 e 7 aparecem apenas em um dos números). Logo o número que obtivemos é 20.
– Após obter junto com os alunos a conclusão acima, utilize as fichas circulares selecionadas para completar a última linha do tabuleiro e procure uma ficha retangular que possa ser utilizada como resultado da multiplicação registrada. Ficaremos com:

– Enfatize que o número obtido (20) é divisor tanto de 180 quanto de 140 (considerando a relação entre divisores e fatoração trabalhada no segundo passo da atividade 1).
– Proponha aos alunos que tentem, acrescentando fichas circulares, obter um outro número que também seja divisor do 180 e do 140. Faça com que percebam a impossibilidade de ter sucesso nesta busca.
– Conclua que 20 não apenas é divisor de 180 e 140, como também é o maior número que é divisor comum a 180 e 140.
– Defina o MDC a partir da atividade desenvolvida:
“O maior divisor comum (MDC) de dois números naturais é o maior número natural que é divisor dos dois números dados”
Logo, o MDC de 180 e 140 é 20. Denotamos:
MDC(180,140) = 20
– Peça aos alunos que reproduzam esta atividade para os exemplos a seguir. Cada um deles deve ser registrado através do preenchimento de um tabuleiro na ficha de acompanhamento 2.
- Hora de registrar: Cada um dos exemplos abaixo deve ser registrado em um tabuleiro da ficha de acompanhamento 2.
1) MDC(4,10)
4 = 2 x 2
10 = 2 x 5
O fator comum é o 2, logo mdc(4,10) = 2
2) MDC(15,18)
15 = 3×5
18 = 2x2x3
O fator comum é o 3, logo mdc(15,18) = 3
3) MDC(12, 28)
12 = 2 x 2 x 3
28 = 2 x 2 x 7
Os fatores comuns são 2 e 2 logo mdc(12, 28) = 2 x 2 = 4
4) MDC(15, 28)
15 = 3 x 5
28 = 2 x 2 x 7
Sobre este exemplo é importante fazer as seguintes observações:
Não há fatores primos comuns. Como vimos no módulo instrucional Entendendo Múltiplos e MMC:
Dois números naturais que não possuem nenhum fator primo em comum são chamados primos entre si.
O MDC de dois números primos entre si é sempre igual a 1.
– Outros exemplos a serem trabalhados pelos alunos:
5) MDC(5,18)
5 = 5
18 = 2 x 3 x 3
Observe que não há fatores primos comuns. Neste caso dizemos que esse números são primos entre si, pois o máximo divisor comum entre eles é 1.
6) MDC(14,28)
14 = 2 x 7
28 = 2 x 2 x 7
Os fatores comuns são 2 e 7, logo mdc(14,28) = 2 x 7 = 14
7) MDC(18, 90)
18 = 2 x 3 x 3
90= 2 x 3 x 3 x 5
Os fatores comuns são 2, 3 e 3, logo mdc(18, 90) = 2 x 3 x 3 = 18
Após este exemplo vale observar que sempre que um número é divisor de outro número o MDC entre os dois coincide com o menor número. Pergunte aos alunos por que isso acontece.
8) MDC(54, 120)
54 = 2 x 3 x 3 x 3
120 = 2 x 2 x 2 x 3 x 5
Os fatores comuns são 2 e 3, logo mdc(54,120) = 2 x 3 = 6
9) MDC(22, 121)
22 = 2 x 11
121 = 11 x 11
O fator comum é o 11, logo mdc(22,121) = 11
O professor pode propor outros exemplos caso note que os alunos ainda não estão dominando a atividade proposta.
ARQUIVOS PARA DOWNLOAD

