
Joselane Rodrigues Santana de Abreu, Cristiana Gomes Nunes e Michelle Dysman
Este trabalho consiste de uma proposta para ensino de adição e subtração através do uso de ábaco. Estas atividades foram desenvolvidas para turmas de sexto ano nas quais diagnosticamos deficiências relacionadas à aprendizagem das operações aritméticas. Para este nível o material aqui apresentado pode ser aplicado ao longo de dois tempos de aula. Pode-se, também, utilizar este material para ensino das operações aritméticas no primeiro ciclo do fundamental, mas nesse caso recomendamos que o trabalho seja feito de forma mais lenta, dividido em várias aulas.
Os principais conteúdos envolvidos nas atividades aqui propostas são: sistema de numeração decimal e adição de naturais e subtração de naturais. Como resultados do desenvolvimento destas atividades em sala de aula vamoscapacitar o aluno a:
· Manusear o ábaco;
· Identificar as ordens do Sistema de Numeração Decimal;
· Entender o conceito de agrupamentos, reagrupamentos e valor posicional;
· Compreender os algoritmos das operações de adição e subtração.
Os recursos necessários para o desenvolvimento destas atividades são ábacos abertos (recomendamos um por aluno) e fichas de acompanhamento (listas de exercícios que fornecemos neste módulo). Através destas mesmas fichas de acompanhamento poderá ser feita a avaliação do trabalho e a verificação de aprendizagem.
Objetivos
Conferir significado aos algoritmos da adição e subtração através da associação de seus diversos passos com as etapas dos procedimentos utilizados para efetuar estas operações no ábaco.
Aprimorar a compreensão dos alunos sobre adição e subtração.
Materiais utilizados
– Ábacos abertos (um por aluno ou dupla);
– Listas de exercícios e acompanhamento fornecidas neste plano.
Etapas do trabalho
1ª atividade: o sistema de numeração decimal e o ábaco aberto
2ª atividade: relacionar a soma no ábaco ao algoritmo da adição
3ª atividade: relacionar a subtração no ábaco ao algoritmo desta operação (sem substituições)
4ª atividade: relacionar a subtração no ábaco ao algoritmo desta operação (com substituições)
Atividades
1ª atividade: o sistema de numeração decimal e o ábaco aberto
Objetivos: ensinar a representação de números naturais no ábaco aberto ressaltando a relação entre posição e valor dos algarismos no sistema decimal.
Materiais: ábaco aberto e ficha de acompanhamento 1 .
O sistema de numeração que utilizamos é o decimal, pois os agrupamentos e reagrupamentos são feitos de dez em dez. Para a utilização do ábaco precisamos compreender as regras básicas do sistema de numeração decimal e, em particular, a ideia de valor posicional: o mesmo algarismo pode representar valores diferentes dependendo da posição que ocupa no número. Por exemplo, o algarismo 1 representa, no número 10, uma dezena, já no número 100, representa uma centena. Essa mesma relação do valor com a posição do algarismo pode ser observada na representação dos números no ábaco aberto:

Assim, o ábaco aberto é o material concreto que usaremos para representar o sistema de numeração decimal. É formado por um pino para as unidades, um para as dezenas, um para as centenas e um para os milhares (alguns ábacos abertos possuem ainda um pino para as dezenas de milhares). Logo cada pino representa uma ordem.
1º PASSO – EXPLICAR AOS ALUNOS O SIGNIFICADO DE CADA PINO DO ÁBACO
· segure um ábaco vazio e uma argola;
· coloque a argola no primeiro pino da direita (unidades);
· pergunte aos alunos que número esta argola representa no ábaco;
·
repita o procedimento para cada um dos pinos (no segundo os alunos
devem responder que a argola representa 10, no terceiro 100 e assim por
diante).
É fundamental que os alunos compreendam muito bem que cada pino representa uma ordem, uma quantidade diferente.
No ábaco realizamos operações básicas tais como: adição, subtração, multiplicação e divisão. Neste módulo instrucional trabalharemos somente com adição e subtração. Para a utilização do ábaco os alunos devem compreender que sempre que temos dez argolas agrupadas em um pino, devemos substituí-las por uma argola no pino seguinte (à esquerda).
2º PASSO – ENSINAR A UTILIZAR O ÁBACO
O professor deve explicar aos alunos que em cada pino só pode haver no máximo nove argolas, e que quando tivermos dez argolas devemos substituí-las por uma argola no pino seguinte. Em seguida deve exemplificar apresentando tais substituições no ábaco: Devemos substituir 10 unidades por 1 dezena.
Devemos substituir 10 dezenas por 1 centena.

Devemos substituir 10 dezenas por 1 centena.

Da mesma forma 10 centenas por uma 1 milhar.

Em seguida o professor deve utilizar alguns exemplos para ensinar aos alunos como representar os números no ábaco. Escreva o número no quadro e pergunte aos alunos quantas unidades, quantas dezenas, quantas centenas e quantos milhares devemos usar para representar este número no ábaco. Oriente os alunos a representarem em seus ábacos o número dado. A seguir apresentamos algumas possibilidades. Caberá ao professor observar as respostas da turma para verificar se são necessários exemplos adicionais. É importante atentar para números que usam o zero em sua representação. Os alunos costumam errar nestes casos não deixando o pino correspondente vazio



- Hora de registrar: As atividades da ficha de acompanhamento 1 devem ser realizadas neste momento.
2ª atividade: relacionar a soma no ábaco ao algoritmo da adição
Para ensinar a adição utilizando o ábaco como recurso pedagógico, é fundamental que o professor articule o trabalho feito sobre o ábaco com as etapas do algoritmo da adição. Sem que esses dois processos sejam realizados simultaneamente, corre-se o risco de que o aluno aprenda a operar sobre o ábaco sem relacionar esta tarefa ao algoritmo que desejamos ensinar (e assim o algoritmo continuaria sendo um processo mecânico desprovido de significado). Veremos como trabalhar em sala de aula para promover pelo uso do ábaco a compreensão do significado dos diferentes passos do algoritmo de adição.
,
1º PASSO – ARMAR A CONTA
Primeiro o professor deve colocar no quadro um exemplo e armar a conta colocando sobre cada algarismo a letra que representa sua ordem:
a) 12 + 9 =
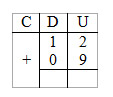
(é importante colocar o zero antes do 9 e explicar aos alunos que isso significa que temos zero dezenas).
2º PASSO – REPRESENTAR A PRIMEIRA PARCELA NO ÁBACO
Em seguida o professor deve pedir aos alunos que representem o primeiro número no ábaco. Logo que os alunos tenham realizado esta tarefa o professor deve representar em seu próprio ábaco para que os alunos confiram.

3º PASSO – ADICIONAR A SEGUNDA PARCELA NO ÁBACO
A seguir pede-se aos alunos que acrescentem 9 argolas às unidades para efetuar a soma.

4º PASSO – RELACIONAR A TROCA DE ARGOLAS AO “VAI-UM”
Pergunta-se quantas argolas ficaram no pino das unidades. Quando responderem 11, perguntamos se podemos ficar com 11 argolas neste pino. Devemos esclarecer que não, que só pode haver no máximo 9 argolas em cada pino, e, portanto, devemos trocar dez argolas de unidades por uma no pino das dezenas.

Simultaneamente explicamos no algoritmo: quando somamos duas unidades mais nove unidades temos como resultado onze unidades, mas não podemos escrever 11 na casa reservada às unidades, então, assim como substituímos 10 unidades por uma dezena no ábaco, devemos “levar uma dezena” para a casa das dezenas (é o “vai um”) e ficamos com uma unidade apenas na casa das unidades. Então temos:
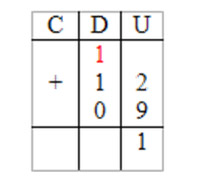
5º PASSO – OBSERVAR E REGISTRAR O RESULTADO
Observamos que o resultado no ábaco conta com duas argolas no pino das dezenas.
Voltamos ao algoritmo para terminar a conta explicando que a dezena que levamos após a substituição se somou no ábaco à dezena proveniente do 12:

6º PASSO – PRATICAR MAIS UM POUCO…
A seguir apresentamos mais alguns exemplos de soma. É importante que o professor conduza o trabalho sempre trabalhando simultaneamente no ábaco e no algoritmo, como explicamos acima. Repita com os alunos estes procedimentos para que fiquem claros.
341 + 19 =
629 +81 =
800 + 308 =
1000 + 350 =
3ª atividade: relacionar a subtração no ábaco ao algoritmo desta operação (sem substituições)
Aqui valem as mesmas observações que fizemos quando tratamos da adição: é fundamental que o professor articule o trabalho feito sobre o ábaco com as etapas do algoritmo da subtração. Sem que esses dois processos sejam realizados simultaneamente, corre-se o risco de que o aluno aprenda a operar sobre o ábaco sem relacionar esta tarefa ao algoritmo que desejamos ensinar (e assim o algoritmo continuaria sendo um processo mecânico desprovido de significado).
1º PASSO – ARMAR A CONTA
Trabalharemos primeiro sobre um exemplo que não exige substituições. O professor deve propor a operação e armar no quadro a conta:
64-23 =

2º PASSO – REPRESENTANDO O MINUENDO NO ÁBACO
Em seguida, no ábaco, junto com os alunos, representamos o 64 (o minuendo)

3º PASSO – SUBTRAÍMOS NO ÁBACO O SUBTRAENDO E RELACIONAMOS AO ALGORITMO
Subtraímos 3 argolas do pino das unidades e duas do pino das dezenas.

Realizamos na conta armada cada um dos passos equivalentes às operações que executamos sobre o ábaco, sempre chamando a atenção para a relação entre o movimento no ábaco e o procedimento na continha (“das quatro argolas das unidades, tiramos três e ficamos com uma, das seis argolas das dezenas, retiramos duas e ficamos com quatro”):
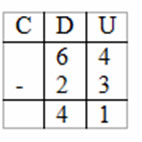
4ª atividade: relacionar a subtração no ábaco ao algoritmo desta operação (conta com substituições)
Em seguida devemos efetuar junto com os alunos algumas subtrações que exijam substituições. Vamos trabalhar com o exemplo 640 – 42.
1º PASSO – ARMANDO A CONTA
Colocamos no quadro a operação e armamos a conta:
640 – 42 =

2º PASSO – REPRESENTANDO O MINUENDO NO ÁBACO
Junto com os alunos, representamos no ábaco o número 640;

3º PASSO – SUBTRAÍMOS NO ÁBACO O SUBTRAENDO E RELACIONAMOS AO ALGORITMO
Em seguida, propomos a retirada de duas unidades. Esperamos que os alunos percebam que não há nenhuma argola no pino das unidades e então propomos a eles que, para que consigamos subtrair as duas unidades é preciso converter uma argola do pino das dezenas em dez argolas no pino das unidades. Após a conversão, ficaremos com:

Agora podemos efetuar a subtração das duas unidades:

Devemos, nesse momento nos voltar para a conta armada e realizar as etapas relacionadas ao que acabamos de fazer no ábaco. Explicamos que não é possível subtrair duas unidades de zero, então “pedimos emprestado” dez unidades para a casa das dezenas, da mesma forma como transformamos no ábaco uma argola das dezenas em dez argolas nas unidades:

Em seguida, precisamos subtrair quatro dezenas e nos deparamos com o mesmo problema de antes: temos apenas 3 dezenas disponíveis. Fazemos no ábaco a substituição necessária (trocando uma centena por dez dezenas) e em seguida demonstramos esse processo no algoritmo:

Finalmente completamos a operação observando que não há centenas a subtrair, logo terminamos com 5 centenas:
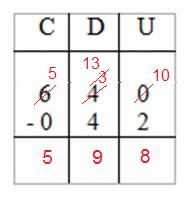
4º PASSO – PRATICANDO MAIS UM POUCO…
Devemos resolver junto com os alunos tantos exemplos quantos sejam necessários e, depois, propor que eles resolvam alguns sozinhos. A seguir sugerimos dois outros exemplos para serem trabalhados como os anteriores.
a) 500 – 208 =
b) 1500 – 350 =
Por fim, recomendamos a aplicação da ficha de acompanhamento sobre adição e subtração com o ábaco.
- Hora de registrar: As atividades da ficha de acompanhamento 2 devem ser realizadas neste momento.
ARQUIVOS PARA DOWNLOAD

